First, we shall embrace Plato's definition of the natural number one. In Republic Ⅶ, Plato says that the natural number one is indivisible, invariable and equal to each other. These three properties are consistent with a human being. First, because everybody is a human being, everybody is equal to each other. Second, a human being is indivisible. Third, a human being is invariable because a human being has been the same person from the birth to the death. These properties of a human being are the base of democracy and humanism. The teacher must teach this fact, and then students would understand the close relationship between mathematics and democracy. Also, students would realize that oneself is a human being, who has the properties of the natural number one. If students recognize these points, they would proceed to the next step. Before that, we shall call the natural number one a unit, because it is the unit of numbers. The teacher will mention a dog and a cat as an example, and then he will teach that an animal has properties of a unit. At an elementary school, because the cell theory is difficult for students, the teacher shall only indicate that the origin of a unit is a life. However, they will recognize the dignity of life.
The Cardinal Number
Next, the teacher shall teach cardinal numbers. The cardinal number is the collection of units. This collection has been called the set, but the word set has too wide meanings. We propose that this collection will be called the basic set. We restrict elements of the basic set to units. That is, the basic set means the cardinal number. For example:
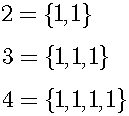
If there is a cardinal number n, then we can make the next cardinal number by adding 1. Using simplified Peano's Axioms, Cardinal numbers are defined as follows:
- 1 is a cardinal number.
- If n is a cardinal number, then n+1 is a cardinal number.
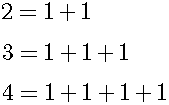
The teacher must get these two forms across to students.
One-to-One Correspondence
Next, the one-to-one correspondence is the important basic concept, but the concept is applied to the too wide range like the set. We propose the basic one-to-one correspondence, which can be applied only between two units. Using the basic one-to-one correspondence, we can compare two cardinal numbers. For example, let us compare 3 with 5. Results are 3 pairs of units and 2 units. This is equivalent to the subtraction:
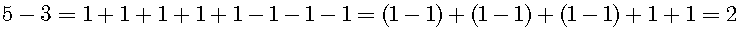
The teacher has to make students to comprehend the basic one-to-one correspondence and the subtraction.
Further, the basic one-to-one correspondence can be applied to the real world. Any object can correspond to a unit. If this correspondence is achieved, the mathematics can be applied to the real world. This is the first step of the practical usage of the mathematics.
The Ordinal Number
The ordinal number is different from the cardinal number. The cardinal number is the collection of units, but the ordinal number is not the collection. For example, let us consider the set of 5 letters: A,B,C,D,E. The cardinal number of the set is 5. If they are aligned in the order of ABCDE, A is the first letter. However, if they are aligned in the order of EDCBA, A is the fifth letter. Furthermore, we can arrange them in the arbitrary sequence. Then, we can rank A as any number. That is, the ordinal number is the number of the place. This fact can apply to units. The cardinal number 5 is collections of 5 units. They are ordered:
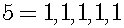
In next equation, square brackets represent the place in the sequence. The number of the place is represented:
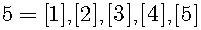
5 on the left-hand side of the equation represents the cardinal number 5, and 5 on the right-hand side of the equation represents the ordinal number 5. Therefore, each unit corresponds to the place number, and any ordinal number has the properties of a unit.
Unsurprisingly, any ordinal number can be put into one-to-one correspondence with another ordinal number, but there is no meaning any more. Early elementary school teachers should not use this type of one-to-one correspondence, and should use the basic one-to-one correspondence.
Cantor says that there is the one-to-one correspondence between even numbers and natural numbers. So, we can match a ordinal number n and a ordinal number 2n.
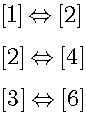
However, this one-to-one correspondence doesn't mean that the numbe of even numbers is the same as the number of natural numbers. According to "What Is Infinity?", no matter how large a natural number is, it is finite. Let us consider a set, which contains all natural nmbers from 1 to 2n. It contains only n even numbers, which are half of all natural numbers in the set.
Next, we cannot match a cardinal number n and a cardinal number 2n.
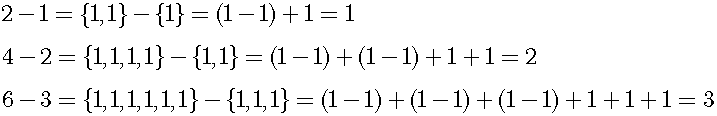
This usage of the one-to-one correspondence is more basic and more useful. Consequently, the concept of the cardinality is nonsense.
Zero
In "What is the natural number one?", I say that the origin of a unit is a life. So, we cannot easily accept the concept of zero, because our mathematics is based on a unit as a life. If there is no life, various situations can be considered. One of the most acceptable conditions for life is the sterile culture medium. Meanwhile, one of the fatal conditions for life is outer space. That is to say, the number zero contains all conditions from best to worst. We cannot regard these conditions as biologically the same condition. Therefore, we can do nothing but define zero arbitrary.
Firstly, zero must not correspond to the fatal condition for life. If we try to add zero to the member of numbers, 0 plus 1 has to be 1. However, if zero means the fatal condition, 0 plus 1 equals 0. Let us take a human being as an example. In a battlefield, 0 plus 1 will be sometimes 0. Zero does not mean the bad condition for human beings, but zero only means that there is no human being in the ordinary condition.
Secondly, we have to argue whether zero has the properties of a unit or not. We shall postulate that zero is invariable and equal to each other. However, zero is divisible:
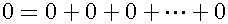
Zero can be divided into an arbitrary number of zeros. That is, zero isn't a unit. Therefore, zero isn't a natural number .